 |
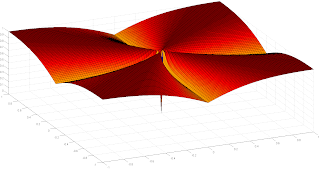
| Smoothed $\ell_1/\ell_2$ function for a sparse $\ell_0$ surrogate |
Mai Quyen PHAM has defended her PhD thesis on July 15th, 2015 at 10.00 am, on the topic of "Seismic wave field restoration using sparse representations and quantitative analysis” (manuscript in pdf), at Université Paris-Est, bâtiment Copernic, amphithéâtre Maurice Gross, 5 boulevard Descartes (RER A, Noisy-Champs), 77420 Champs-sur-Marne.
Its focus is twofold:
1) sparse adaptive filtering with approximate templates in redundant and geometric wavelet frames (akin to echo cancellation in speech),
Its focus is twofold:
1) sparse adaptive filtering with approximate templates in redundant and geometric wavelet frames (akin to echo cancellation in speech),
2) sparse blind deconvolution for parsimonious reflectivity signals with l1/l2 norm ratio penalty
This work has notably been published in two journal papers
*Euclid in a Taxicab: Sparse Blind Deconvolution with Smoothed l_1/l_2
Audrey Repetti, Mai Quyen-Pham, Laurent Duval, Émilie Chouzenoux, Jean-Christophe Pesquet
IEEE Signal Processing Letters, May 2015, Volume 22, Number 5, pages 539-543.
http://dx.doi.org/10.1109/LSP.2014.2362861
Abstract: The l1/l2 ratio regularization function has shown good performance for retrieving sparse signals in a number of recent works, in the context of blind deconvolution. Indeed, it benefits from a scale invariance property much desirable in the blind context. However, the l1/l2 function raises some difficulties when solving the nonconvex and nonsmooth minimization problems resulting from the use of such a penalty term in current restoration methods. In this paper, we propose a new penalty based on a smooth approximation to the l1/l2 function. In addition, we develop a proximal-based algorithm to solve variational problems involving this function and we derive theoretical convergence results. We demonstrate the effectiveness of our method through a comparison with a recent alternating optimization strategy dealing with the exact l1/l2 term, on an application to seismic data blind deconvolution.
*A Primal-Dual Proximal Algorithm for Sparse Template-Based Adaptive Filtering: Application to Seismic Multiple Removal
Mai-Quyen Pham, Laurent Duval, Caroline Chaux, Jean-Christophe Pesquet
IEEE Transactions on Signal Processing, August 2014, Volume 62, Issue 16, pages 4256-4269
http://dx.doi.org/10.1109/TSP.2014.2331614
PhD Committee:
Reporter Jean-Francois Aujol Prof. Université de Bordeaux
Reporter Mauricio D Sacchi Prof. University of Alberta
Examiner Jérôme Mars Prof. Grenoble-INP
Examiner Mai K. Nguyen Prof. Université de Cergy-Pontoise
PhD supervisor Jean-Christophe Pesquet Prof. Université Paris-Est Marne-la-Vallée
PhD co-supervisor Laurent Duval Dr. IFP Energies nouvelles (IFPEN)
PhD co-supervisor Caroline Chaux CNRS researcher, I2M, Aix-Marseille Université
Mai-Quyen Pham, Laurent Duval, Caroline Chaux, Jean-Christophe Pesquet
IEEE Transactions on Signal Processing, August 2014, Volume 62, Issue 16, pages 4256-4269
http://dx.doi.org/10.1109/TSP.2014.2331614
PhD Committee:
Reporter Jean-Francois Aujol Prof. Université de Bordeaux
Reporter Mauricio D Sacchi Prof. University of Alberta
Examiner Jérôme Mars Prof. Grenoble-INP
Examiner Mai K. Nguyen Prof. Université de Cergy-Pontoise
PhD supervisor Jean-Christophe Pesquet Prof. Université Paris-Est Marne-la-Vallée
PhD co-supervisor Laurent Duval Dr. IFP Energies nouvelles (IFPEN)
PhD co-supervisor Caroline Chaux CNRS researcher, I2M, Aix-Marseille Université


